Poker Hand Combinations Probability

4/9/2022 admin

POKER PROBABILITIES

In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands. Thus, the number of high card hands is 1,499(16,384 - 844)=23,294,460. If we sum the preceding numbers, we obtain 133,784,560 and we can be confident the numbers are correct. Here is a table summarizing the number of 7-card poker hands. The probability is the probability of having the hand dealt to you when dealt 7 cards. Probability of being dealt a certain starting hand There are a total of exactly 1,326 different starting hand combinations in Texas Hold’em poker. However, many of them are practically identical, e.g. A♥K♣ is exactly the same hand as A♦K♠ before the flop.

Texas Hold'em Poker
Texas Hold'em Poker probabilities
Omaha Poker
Omaha Poker probabilities
5 Card Poker
5 Card Poker probabilities

POKER CALCULATOR

Poker calculator
Poker odds calculator

POKER INFORMATION

Poker hand rankings
Ranking of poker hands

In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands.

Frequency of 5-card poker hands

The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement. Wild cards are not considered. The probability of drawing a given hand is calculated by dividing the number of ways of drawing the hand by the total number of 5-card hands (the sample space, five-card hands). The odds are defined as the ratio (1/p) - 1 : 1, where p is the probability. Note that the cumulative column contains the probability of being dealt that hand or any of the hands ranked higher than it. (The frequencies given are exact; the probabilities and odds are approximate.)

The nCr function on most scientific calculators can be used to calculate hand frequencies; entering nCr with 52 and 5, for example, yields as above.

Hand	Frequency	Approx. Probability	Approx. Cumulative	Approx. Odds
Royal flush	4	0.000154%	0.000154%	649,739 : 1
Straight flush (excluding royal flush)	36	0.00139%	0.00154%	72,192.33 : 1
Four of a kind	624	0.0240%	0.0256%	4,164 : 1
Full house	3,744	0.144%	0.170%	693.2 : 1
Flush (excluding royal flush and straight flush)	5,108	0.197%	0.367%	507.8 : 1
Straight (excluding royal flush and straight flush)	10,200	0.392%	0.76%	253.8 : 1
Three of a kind	54,912	2.11%	2.87%	46.3 : 1
Two pair	123,552	4.75%	7.62%	20.03 : 1
One pair	1,098,240	42.3%	49.9%	1.36 : 1
No pair / High card	1,302,540	50.1%	100%	.995 : 1
Total	2,598,960	100%	100%	1 : 1

The royal flush is a case of the straight flush. It can be formed 4 ways (one for each suit), giving it a probability of 0.000154% and odds of 649,739 : 1.

When ace-low straights and ace-low straight flushes are not counted, the probabilities of each are reduced: straights and straight flushes each become 9/10 as common as they otherwise would be. The 4 missed straight flushes become flushes and the 1,020 missed straights become no pair.

Note that since suits have no relative value in poker, two hands can be considered identical if one hand can be transformed into the other by swapping suits. For example, the hand 3♣ 7♣ 8♣ Q♠ A♠ is identical to 3♦ 7♦ 8♦ Q♥ A♥ because replacing all of the clubs in the first hand with diamonds and all of the spades with hearts produces the second hand. So eliminating identical hands that ignore relative suit values, there are only 134,459 distinct hands.

The number of distinct poker hands is even smaller. For example, 3♣ 7♣ 8♣ Q♠ A♠ and 3♦ 7♣ 8♦ Q♥ A♥ are not identical hands when just ignoring suit assignments because one hand has three suits, while the other hand has only two—that difference could affect the relative value of each hand when there are more cards to come. However, even though the hands are not identical from that perspective, they still form equivalent poker hands because each hand is an A-Q-8-7-3 high card hand. There are 7,462 distinct poker hands.

Derivation of frequencies of 5-card poker hands

of the binomial coefficients and their interpretation as the number of ways of choosing elements from a given set. See also: sample space and event (probability theory).

Straight flush — Each straight flush is uniquely determined by its highest ranking card; and these ranks go from 5 (A-2-3-4-5) up to A (10-J-Q-K-A) in each of the 4 suits. Thus, the total number of straight flushes is:
- Royal straight flush — A royal straight flush is a subset of all straight flushes in which the ace is the highest card (ie 10-J-Q-K-A in any of the four suits). Thus, the total number of royal straight flushes is
  or simply . Note: this means that the total number of non-Royal straight flushes is 36.

Four of a kind — Any one of the thirteen ranks can form the four of a kind by selecting all four of the suits in that rank. The final card can have any one of the twelve remaining ranks, and any suit. Thus, the total number of four-of-a-kinds is:

Full house — The full house comprises a triple (three of a kind) and a pair. The triple can be any one of the thirteen ranks, and consists of three of the four suits. The pair can be any one of the remaining twelve ranks, and consists of two of the four suits. Thus, the total number of full houses is:

Flush — The flush contains any five of the thirteen ranks, all of which belong to one of the four suits, minus the 40 straight flushes. Thus, the total number of flushes is:

Straight — The straight consists of any one of the ten possible sequences of five consecutive cards, from 5-4-3-2-A to A-K-Q-J-10. Each of these five cards can have any one of the four suits. Finally, as with the flush, the 40 straight flushes must be excluded, giving:

Three of a kind — Any of the thirteen ranks can form the three of a kind, which can contain any three of the four suits. The remaining two cards can have any two of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of three-of-a-kinds is:

Two pair — The pairs can have any two of the thirteen ranks, and each pair can have two of the four suits. The final card can have any one of the eleven remaining ranks, and any suit. Thus, the total number of two-pairs is:

Poker hand combinations probability formula

Pair — The pair can have any one of the thirteen ranks, and any two of the four suits. The remaining three cards can have any three of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of pair hands is:

No pair — A no-pair hand contains five of the thirteen ranks, discounting the ten possible straights, and each card can have any of the four suits, discounting the four possible flushes. Alternatively, a no-pair hand is any hand that does not fall into one of the above categories; that is, any way to choose five out of 52 cards, discounting all of the above hands. Thus, the total number of no-pair hands is:

Any five card poker hand — The total number of five card hands that can be drawn from a deck of cards is found using a combination selecting five cards, in any order where n refers to the number of items that can be selected and r to the sample size; the '!' is the factorial operator:

This guide is licensed under the GNU Free Documentation License. It uses material from the Wikipedia.

Home > 5 Card Poker probabilities

Introduction

Derivations for Five Card Stud

I have been asked so many times how I derived the probabilities of drawing each poker hand that I have created this section to explain the calculation. This assumes some level mathematical proficiency; anyone comfortable with high school math should be able to work through this explanation. The skills used here can be applied to a wide range of probability problems.

The Factorial Function

If you already know about the factorial function you can skip ahead. If you think 5! means to yell the number five then keep reading.

The instructions for your living room couch will probably recommend that you rearrange the cushions on a regular basis. Let's assume your couch has four cushions. How many combinations can you arrange them in? The answer is 4!, or 24. There are obviously 4 positions to put the first cushion, then there will be 3 positions left to put the second, 2 positions for the third, and only 1 for the last one, or 4*3*2*1 = 24. If you had n cushions there would be n*(n-1)*(n-2)* ... * 1 = n! ways to arrange them. Any scientific calculator should have a factorial button, usually denoted as x!, and the fact(x) function in Excel will give the factorial of x. The total number of ways to arrange 52 cards would be 52! = 8.065818 * 10⁶⁷.

The Combinatorial Function

Assume you want to form a committee of 4 people out of a pool of 10 people in your office. How many different combinations of people are there to choose from? The answer is 10!/(4!*(10-4)!) = 210. The general case is if you have to form a committee of y people out of a pool of x then there are x!/(y!*(x-y)!) combinations to choose from. Why? For the example given there would be 10! = 3,628,800 ways to put the 10 people in your office in order. You could consider the first four as the committee and the other six as the lucky ones. However you don't have to establish an order of the people in the committee or those who aren't in the committee. There are 4! = 24 ways to arrange the people in the committee and 6! = 720 ways to arrange the others. By dividing 10! by the product of 4! and 6! you will divide out the order of people in an out of the committee and be left with only the number of combinations, specifically (1*2*3*4*5*6*7*8*9*10)/((1*2*3*4)*(1*2*3*4*5*6)) = 210. The combin(x,y) function in Excel will tell you the number of ways you can arrange a group of y out of x.

Now we can determine the number of possible five card hands out of a 52 card deck. The answer is combin(52,5), or 52!/(5!*47!) = 2,598,960. If you're doing this by hand because your calculator doesn't have a factorial button and you don't have a copy of Excel, then realize that all the factors of 47! cancel out those in 52! leaving (52*51*50*49*48)/(1*2*3*4*5). The probability of forming any given hand is the number of ways it can be arranged divided by the total number of combinations of 2,598.960. Below are the number of combinations for each hand. Just divide by 2,598,960 to get the probability.

Poker Math

The next section shows how to derive the number of combinations of each poker hand in five card stud.

Royal Flush

There are four different ways to draw a royal flush (one for each suit).

Straight Flush

The highest card in a straight flush can be 5,6,7,8,9,10,Jack,Queen, or King. Thus there are 9 possible high cards, and 4 possible suits, creating 9 * 4 = 36 different possible straight flushes.

Four of a Kind

There are 13 different possible ranks of the 4 of a kind. The fifth card could be anything of the remaining 48. Thus there are 13 * 48 = 624 different four of a kinds.

Full House

There are 13 different possible ranks for the three of a kind, and 12 left for the two of a kind. There are 4 ways to arrange three cards of one rank (4 different cards to leave out), and combin(4,2) = 6 ways to arrange two cards of one rank. Thus there are 13 * 12 * 4 * 6 = 3,744 ways to create a full house.

Poker hand combinations probability table

Flush

There are 4 suits to choose from and combin(13,5) = 1,287 ways to arrange five cards in the same suit. From 1,287 subtract 10 for the ten high cards that can lead a straight, resulting in a straight flush, leaving 1,277. Then multiply for 4 for the four suits, resulting in 5,108 ways to form a flush.

Straight

The highest card in a straight can be 5,6,7,8,9,10,Jack,Queen,King, or Ace. Thus there are 10 possible high cards. Each card may be of four different suits. The number of ways to arrange five cards of four different suits is 4⁵ = 1024. Next subtract 4 from 1024 for the four ways to form a flush, resulting in a straight flush, leaving 1020. The total number of ways to form a straight is 10*1020=10,200.

Three of a Kind

There are 13 ranks to choose from for the three of a kind and 4 ways to arrange 3 cards among the four to choose from. There are combin(12,2) = 66 ways to arrange the other two ranks to choose from for the other two cards. In each of the two ranks there are four cards to choose from. Thus the number of ways to arrange a three of a kind is 13 * 4 * 66 * 4² = 54,912.

Two Pair

There are (13:2) = 78 ways to arrange the two ranks represented. In both ranks there are (4:2) = 6 ways to arrange two cards. There are 44 cards left for the fifth card. Thus there are 78 * 6² * 44 = 123,552 ways to arrange a two pair.

One Pair

There are 13 ranks to choose from for the pair and combin(4,2) = 6 ways to arrange the two cards in the pair. There are combin(12,3) = 220 ways to arrange the other three ranks of the singletons, and four cards to choose from in each rank. Thus there are 13 * 6 * 220 * 4³ = 1,098,240 ways to arrange a pair.

Nothing

First find the number of ways to choose five different ranks out of 13, which is combin(13,5) = 1287. Then subtract 10 for the 10 different high cards that can lead a straight, leaving you with 1277. Each card can be of 1 of 4 suits so there are 4⁵=1024 different ways to arrange the suits in each of the 1277 combinations. However we must subtract 4 from the 1024 for the four ways to form a flush, leaving 1020. So the final number of ways to arrange a high card hand is 1277*1020=1,302,540.

Specific High Card

For example, let's find the probability of drawing a jack-high. There must be four different cards in the hand all less than a jack, of which there are 9 to choose from. The number of ways to arrange 4 ranks out of 9 is combin(9,4) = 126. We must then subtract 1 for the 10-9-8-7 combination which would form a straight, leaving 125. From above we know there are 1020 ways to arrange the suits. Multiplying 125 by 1020 yields 127,500 which the number of ways to form a jack-high hand. For ace-high remember to subtract 2 rather than 1 from the total number of ways to arrange the ranks since A-K-Q-J-10 and 5-4-3-2-A are both valid straights. Here is a good site that also explains how to calculate poker probabilities.

Five Card Draw — High Card Hands

Hand	Combinations	Probability
Ace high	502,860	0.19341583
King high	335,580	0.12912088
Queen high	213,180	0.08202512
Jack high	127,500	0.04905808
10 high	70,380	0.02708006
9 high	34,680	0.01334380
8 high	14,280	0.00549451
7 high	4,080	0.00156986
Total	1,302,540	0.501177394

Ace/King High

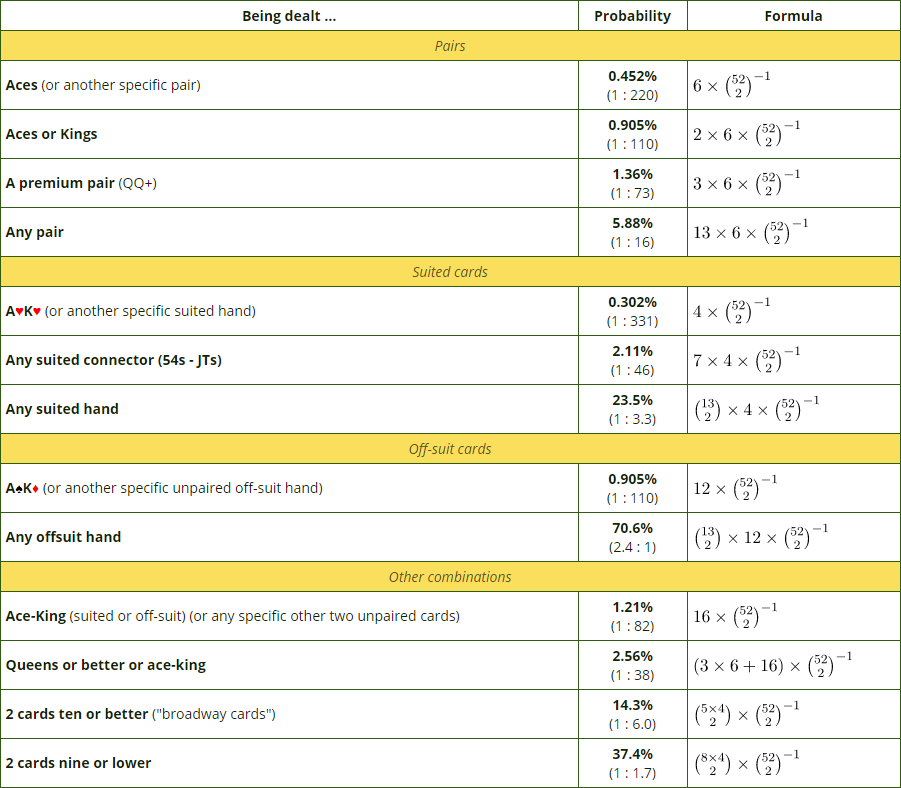
For the benefit of those interested in Caribbean Stud Poker